Chapter 3: Distance Measurement#
Parallax#
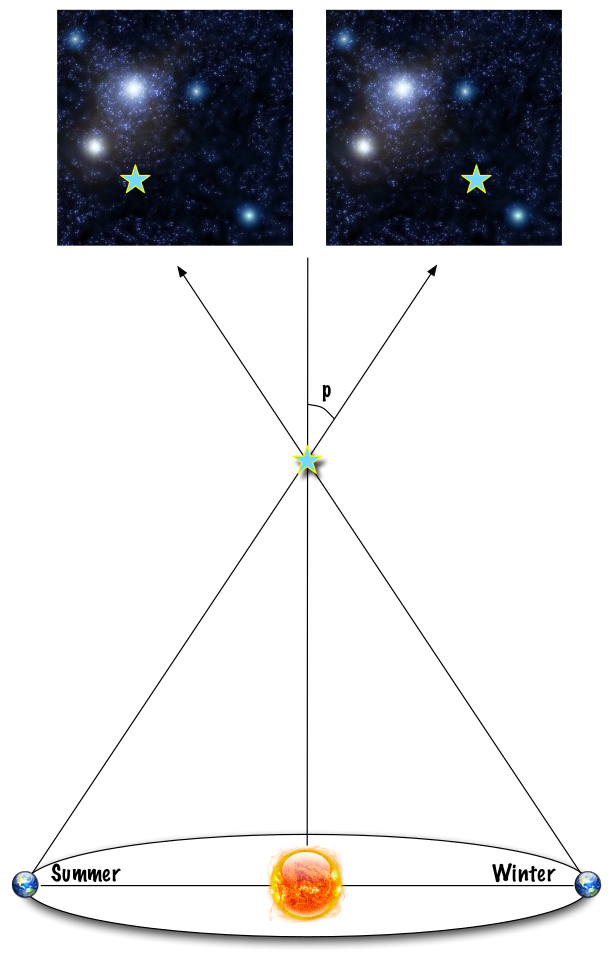
Fig. 9 parallax schematic on sky#
parallax schematic trigonometry
Parallax is the name given to the phenomenon where an object appears to move, relative to the background, when viewed along two different lines of sight. Parallax is easily experienced by holding your thumb up at arms length and then closing one eye, and then the other. Your thumb appears to move relative to the background. The effects of parallax mean that each eye sees a subtly different scene; having two eyes with overlapping fields of view is what allows your brain to measure the distances to everyday objects and gives you depth perception. Therefore, you are already an expert in applying parallax to measure distance, and what follows will surely be simple revision.
In astrophysics, parallax is the only method we have for obtaining direct measures of distance for objects outside our solar system. The way it works is illustrated in figure 9. As the Earth moves round the Sun, we observe different lines of sight towards a nearby star. Because nearby objects experience larger parallax than further objects (it should be obvious why, from figure 9), the nearby star appears to move, relative to the distant, background stars. From the right hand side of figure 9, we can see that
Since \(p\) is such a small angle, we can use the small angle approximation, \(\tan p \approx p\), where p is measured in radians, to get
We can make life much easier for ourselves by some careful choice of units. For a start, parallax angles are so small that a radian is an awkward unit. We would be better off using arcseconds – Just like an hour is divided into minutes and seconds, so a degree is divided into arcminutes and arcseconds. \(1^{\circ} = 60 \, \text{arcminutes} \, (60')\), \(1' = 60 \, \text{arcseconds} \, (60'')\), so \(1^{\circ} = 60 \times 60 = 3600''\) – Also, the Earth-Sun distance and typical stellar distances are too large to be easily measured in metres. What we will do is define a new unit, the parsec, so that an object at a distance of 1 parsec (1 pc) will have a parallax of 1 arcsecond. If we do this, the parallax equation becomes
How large is a parsec? Basic trigonometry reveals that a parsec is 206,265 AU, \(3.085\times 10^{16}\) m, or 3.28 light years. It is a very convenient unit for distances in astronomy.
Typical parallaxes#
How large is the parallax for our nearest star? Proxima Centauri has a parallax of \(p=0''.75\), which corresponds to a distance of \(d=1.33\) pc. This is a very small amount of parallax; roughly the same angle as that subtended by a 2 pence piece at a distance of 5km! This is comparable to the resolution of ground-based telescopes. In principle the diffraction limit of a telescope, θ, in radians, depends on the observed wavelength (λ) and diameter (\(D\)) of the telescope via
For the Hicks 16\(''\) telescope (\(D\) = 0.4 m) observing in the \(V\)-band, the theoretical diffraction limit is θ = 0.35 arcsec. In practice, ground based observations are limited by seeing (several arcsec from the roof of the Hicks, but 0.5–1 arcsec at observatories in Chile, Hawaii and La Palma). In other words, even for the nearest stars, we’re looking for a shift in position which is comparable to the size of the stellar image itself. Parallax is a very small effect, which requires extremely careful data taking and analysis to use.
As an historical aside, the difficulty of observing parallax was one of the main reasons the Heliocentric model of the Solar System took so long to be accepted. In general, people assumed that the stars were not much further away than the planets of our own Solar System. Since they didn’t show large parallaxes, the logical conclusion was that the Earth itself did not move. The first succesful measurement of stellar parallax did not come until 1838, when Friedrich Bessel measured the parallax of 61 Cygni to be \(\sim 0''.3\). Modern measurements of parallax have achieved an astonishing level of accuracy. By moving to space, we can overcome the blurring effects of the atmosphere and measure very small shifts in stellar positions. Up until recently, the highest precision of stellar parallaxes was achieved by the Hipparcos satellite, which achieved accuracies of \(\pm 0.001\) arcseconds (± 1 milliarcsec) for the brightest stars. The current state of the art is ESA’s Gaia satellite, whose third data release (DR3) achieved precisions of \(\pm 0.00003\) arcseconds (± 0.03 milliarcsec) for 15th magnitude stars, with parallaxes for 1,467,744,818 sources(!).
It should be clear that parallax is only useful for measuring the distance to nearby stars. Even at the accuracy provided by Gaia DR3, we can only measure reliable distances for stars closer than a few kpc. In order to measure the distance of the furthest stars, and to have any hope of measuring distances to galaxies, we need to apply new techniques.
“Standard Candles” and the Distance Ladder#
A standard candle is the name given to an object of accurately known luminosity. Before going on to describe some types of standard candle, we should ask why they are so useful? The reason is that we can easily measure the flux of these objects from Earth and, if the luminosity is known, we can apply the inverse square law to find the distance
In order to establish that an object is a standard candle, we need some way of knowing its luminosity. That means that, for at least some objects, we already know the distance. Thus, ultimately, all distances from standard candles are based upon distances obtained from parallax. Thus, we might discover a standard candle in our own Galaxy and measure the distance using parallax. Because the luminosity of our standard candle is known, we could use these standard candles to measure the distances to nearby galaxies. In these galaxies, we may find another type of standard candle. Perhaps it is much brighter, allowing us to measure the distance to even further galaxies, and so on. In this manner, we build up a “distance ladder” which enables us to measure distances to all objects, right out to the edge of the Universe. Ultimately though, they are all based on distances measured in our own Galaxy, through parallax.
A standard candle example: Cepheid Variables#
Let’s look at standard candles in more detail by considering a specific, and important, example. Cepheid variables are pulsating stars, whose brightness varies periodically. They are very bright, and can be seen at great distances.
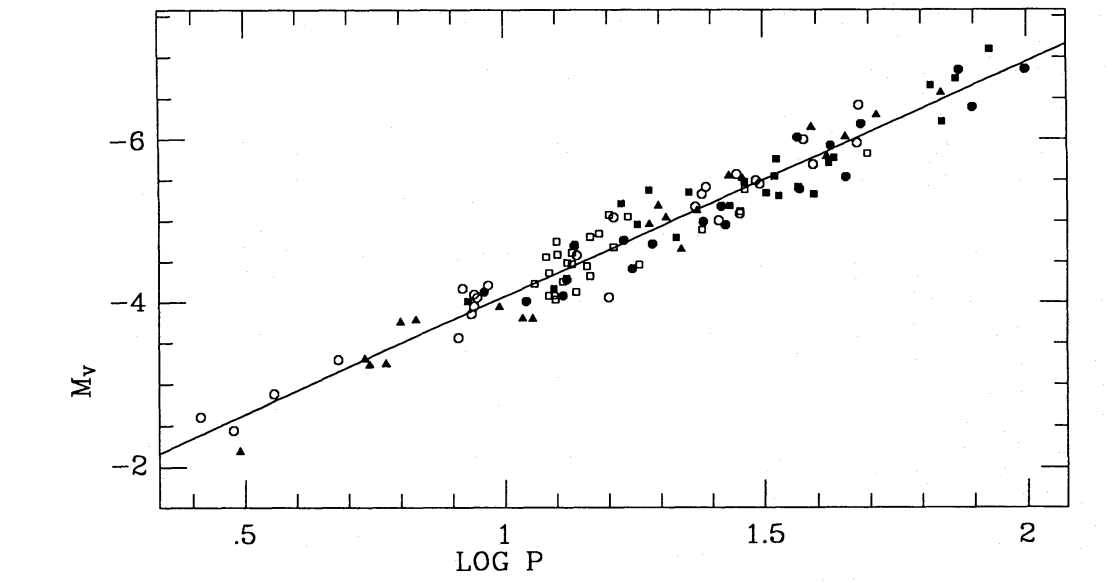
Fig. 10 Calibration of the Cepheid period-luminosity relationship from Lane & Stobie (1994). Here, the logarithm of the period (in days) is shown against the absolute magnitude. The distance to any Cepheid can be found by measuring its period and using this relationship to infer its absolute magnitude. This is compared to the measured apparent magnitude to yield a distance modulus, and hence a distance.#
Cepheid period-luminosity relationship
In 1893, Henrietta Leavitt began work measuring the brightness of stars in the Magellanic Clouds – At that time, women did much work in astrophysics, but they were usually carrying out the laborious lab work and number crunching for male professors. These “computers”, as they were called, rarely received direct credit for their work – In 1908 she published her results, noting a large number of periodic variable stars which showed a pattern; the brighter stars seemed to have longer periods. In 1912 she published another study showing that these variables - Cepheid Variables - showed a close and predictable relationship between their luminosity and the period. In 1913, Hertzsprung used parallax to measure the distance to several Cepheids in our Galaxy. In this way, the relationship between luminosity and period was calibrated. As a result, if the period of a Cepheid Variable could be measured, then the luminosity is known, and the distance to the Cepheid variable can be measured. Today, the relationship is very well established by studying Cepheid variables with known parallaxes from Hipparchos (see figure 10).
At the time of Leavitt’s discovery, it still wasn’t clear that what we know call Galaxies were actually outside of our own Milky Way. Soon, however, Cepheids started to be discovered in other Galaxies. In 1923 Edwin Hubble used Cepheids in the Andromeda Galaxy to show that it was located far outside our Milky Way. In this way Cepheid variables revolutionalised our understanding of the Universe.
Type Ia Supernovae#
Cepheid Variables are bright; whilst the best parallaxes can yield distances to 1 kpc, Cepheids can be observed up to 10-20 Mpc (1 Mpc = 1 million pc). There are other types of variable stars which can be used as standard candles in a similar way to Cepheids (notably the RR Lyrae stars and W Virginis stars), but these are fainter than Cepheids. If we wish to measure the distance to the furthest galaxies, we will need to find another rung on the distance ladder. This rung comes from Type Ia supernovae.
Type Ia supernovae are the explosions on white dwarf stars in binary systems. White dwarfs have a maximum mass, known as the Chandrasekhar limit. This is somewhere around \(1.4 M_{\odot}\). If a white dwarf in a binary system accretes mass from it’s companion, it can be pushed over the Chandrasekhar limit. The white dwarf must then collapse, but the collapse causes the centre of the white dwarf to become extremely dense and hot, which triggers explosive nuclear burning in the core. The resulting supernovae explosion is **extremely ** bright; it is about 14 magnitudes brighter than the brightest Cepheid variable.
Using the general form of equation (7), we can see that type Ia supernovae can be seen to much larger distances than Cepheids. Suppose we have an object on the very limit of visibility, which we then make 14 magnitudes brighter. Now, we move it away until it is once again at the very limit of visibility. How far has it moved?
Type Ia supernovae can be seen 630 times further away than a Cepheid variable! Since Cepheids can be seen to a distance of 20 Mpc, we can see type Ia supernovae to over 10,000 Mpc; that is a significant fraction of the entire visible Universe!
But are type Ia supernovae standard candles? In fact, there is a good reason to believe they are. Since no white dwarf can exceed the Chandrasekhar mass, all type Ia supernovae result from the explosion of a white dwarf at exactly the Chandrasekhar mass. Therefore, we can reasonably expect them all to share the same luminosity! By combining parallax, Cepheid variables and type Ia supernovae, we now have a distance ladder which covers almost the entire Universe. Figure 11 provides an overview of the distance scale of the Universe.
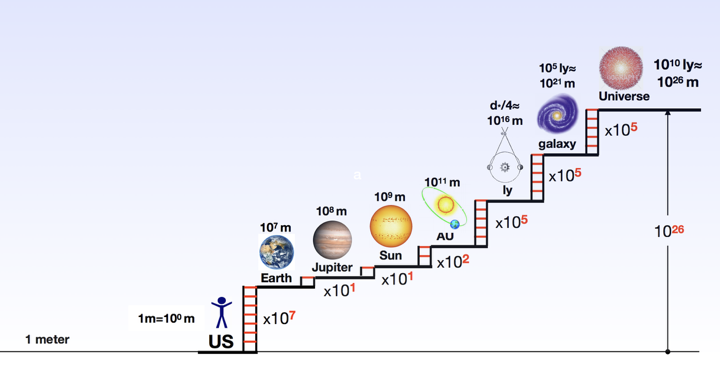
Fig. 11 Distance scale of the Universe, spanning 26 orders of magnitude. Courtesy Stan Owocki (Bartol).#
Distance Scale of the Universe
