Chapter 4: Motion of celestial objects#
Proper Motion and tangential velocity#
The stars are in constant motion. Much of it is apparent motion. Each night, the stars appear to move because of the rotation of the Earth (usually called diurnal motion). Over the course of a year the Earth moves round the Sun, causing the stars which are visible from night to night to change. And finally, as we have discussed, the Earth’s motion around the Sun causes the position of nearby stars to change, due to the phenomenon of parallax.
Once all these apparent sources of motion have been put together however, the stars still move! A star’s motion through space is unsurprisingly called its space velocity. Viewed from Earth, this velocity can be broken down into two components. The component along our line of site is called the radial velocity (\(v_{\rm r}\)), which we will discuss in more detail shortly. The second component lies in the plane of the night sky, and is called the proper motion - see figure 12. The proper motion is visible as a gradual shift in the position of a star, relative to the stars around it. It is convenient to measure it as the rate of angular displacement of the star, in arcseconds/yr, from which the tangential velocity, \(v_{\rm t}\) can be obtained via
where μ is the proper motion in arcsec/yr, \(p\) is the parallax in arcsec and the comversion from AU/yr to km/s can be obtained from the velocity of the Earth around the Sun (since 2\(\pi\) AU/yr = 29.8 km/s).
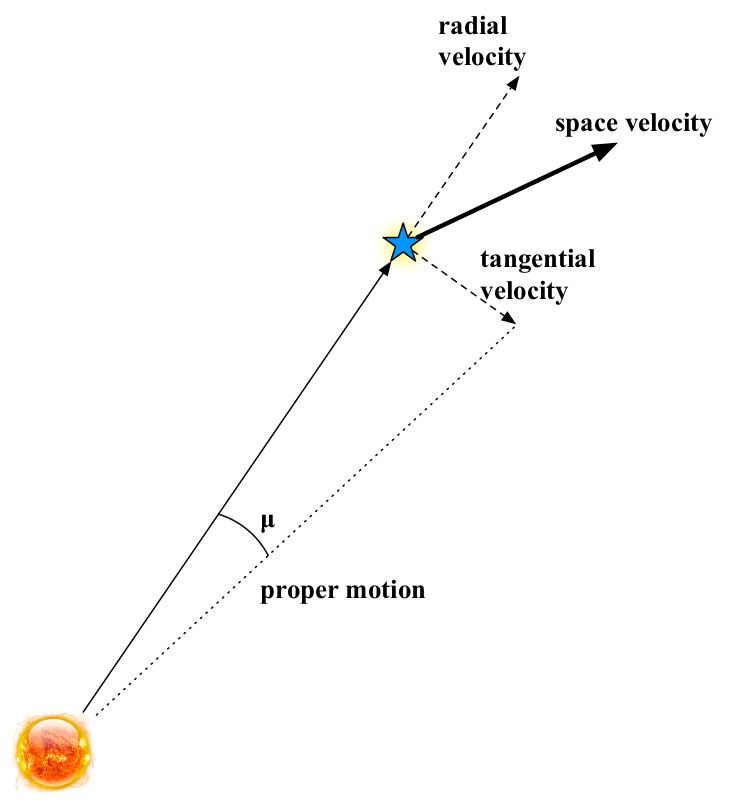
Fig. 12 Stellar motion#
Stellar motion
Proper motions of stars are generally quite small. The star with the largest proper motion, Barnard’s star, moves around 10.3 arcseconds every year. Nevertheless over significant periods of time, the proper motions of stars can build up to quite significant changes. Because a star’s proper motion is measured in arcseconds/yr, a star which is very far away can show a small proper motion, even if it is moving rather fast across our line of sight. Therefore, proper motions are extremely useful for making a sample of stars which are nearby, but become increasingly hard to measure for objects which are far away. Nevertheless, ESA’s Gaia satellite is capable of measuring extremely small proper motions as well as parallax measurements, with typical uncertainties of ± 0.00006 arcseconds per year, such that it is capable of identifying the motion of stars in distant galaxies such as the Large Magellanic Cloud, from which its clockwise rotation can be seen, as illustrated in Fig. 13.

Fig. 13 Rotation of the Large Magellanic Cloud from Gaia DR2 proper motions of individual stars. Credit: Gaia Data Processing and Analysis Consortium (DPAC); A. Moitinho / A. F. Silva / M. Barros / C. Barata, University of Lisbon, Portugal; H. Savietto, Fork Research, Portugal; P. McMillan, Lund Observatory, Sweden#
Large Magellanic Cloud rotation from Gaia proper motions
Radial velocity and Doppler shift#
We return now to the component of the space velocity which is directed along our line of sight; the radial velocity. How do we measure this? A star which has no proper motion but high radial velocity does not appear to move in the night sky… Fortunately, we can measure the radial velocity of celestial objects using the Doppler shift.
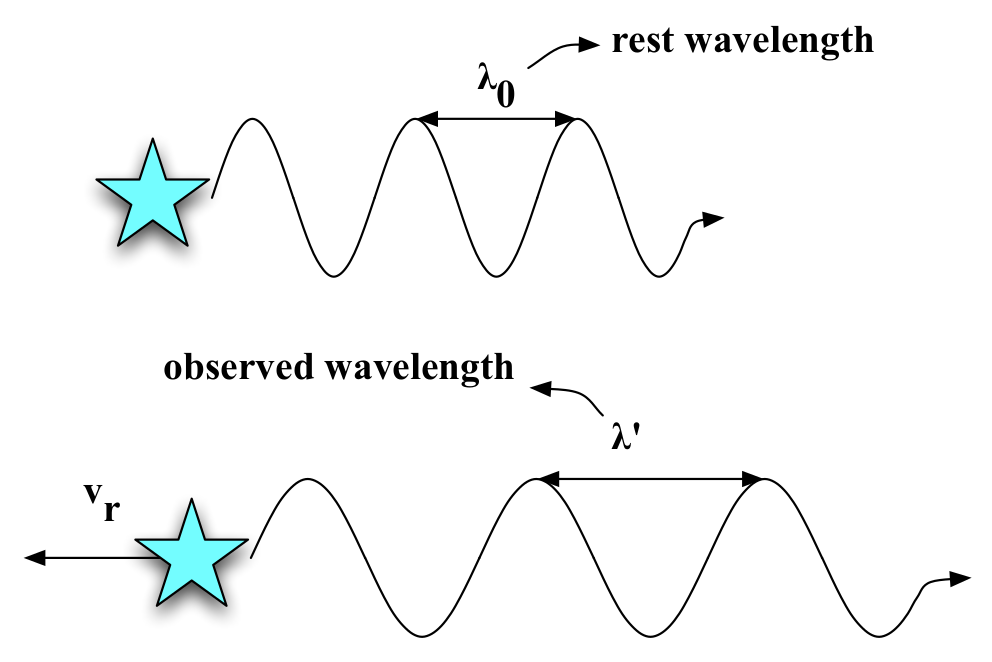
Fig. 14 Doppler shift#
Doppler shift
The cause of the Doppler shift is shown in figure 14. Imagine a star which is moving away from us as it emits light. We can think of the light as being stretched out because of the movement of the star. We can work out how much the light is stretched out using some simple maths. What is the time taken by the star to emit one wavelength of light? Let us call the wavelength emitted by an object at rest \(\lambda_0\). Since the wave travels at the speed of light, the time between peaks is given by
Now consider the star as it moves away from us, with a radial velocity of \(v_r\). It still takes the same time to emit one wave, \(\Delta t\). However, in that time, the star itself has moved a distance
The distance between successive peaks of the light is given by the old wavelength \(\lambda_0\), plus the extra distance moved by the star. So the new wavelength, \(\lambda^{\prime}\), is given by
or, rearranging,
The quantity \(\Delta \lambda\) is called the Doppler shift. An object moving away from us has a positive value of \(v_r\). That means the Doppler shift is positive, the wavelength increases, and so the emitted light becomes increasingly red. We say the light has been redshifted. Conversely, if an object moves towards us the emitted wavelength becomes shorter, and the light is blueshifted.
Measuring Doppler shifts#

Fig. 15 Measuring Doppler shift#
Measuring Doppler shift
How do we measure Doppler shifts? We can do it by taking a spectrum of the source, as illustrated in figure 15. Astronomical spectra often show sharp features at an easily measured wavelength (e.g. absorption or emission lines). In many cases, the rest wavelengths of these lines are known from laboratory experiments performed on Earth, so by comparing the rest wavelength with the observed wavelength from the spectrum, we can easily calculate the Doppler shift.
The true space velocity of a star, \(v_{s}\), can be obtained via
Barnard’s star has a radial velocity if -111 km/s, so its space velocity is 143 km/s. The fastest moving stars in our Galaxy have space velocities of order 300 km s-1, while hypervelocity stars have even more extreme velocities of 1000 km s-1, which are believed to originate in close encounters with the supermassive black hole in the centre of the Milky Way.
The expansion of the Universe#
The combination of measuring Doppler shifts together with the work done on the distance ladder lead directly to one of the most important discoveries made in Astrophysics. Following on from his work in which he used Cepheid Variables to measure the distance of the Andromeda galaxy, Edwin Hubble began work combining the distances to galaxies (as measured by Cepheids), with the velocity at which the galaxies were moving away from us (measured by Doppler shifts). Hubble used a measure called the redshift,
which is proportional to the speed at which the galaxy is moving away from us. Using the 100 inch (2.5m) telescope at the Mount Wilson observatory, Hubble collected redshifts and distances for 46 galaxies. They discovered a proportionality between the redshift and the distance. Since the redshift is proportional to the velocity, this means that the radial velocity of galaxies are proportional to the distance from us, a result now known as Hubble’s law
where \(H_0\) is a constant of proportionality known as Hubble’s constant. Hubble made several mistakes in his work, including getting all his distances wrong, so that his estimate of Hubble’s constant was out by nearly a factor of 10! Nevertheless, the observations changed our view of the Universe forever. At first glance, the result seems staggering. Every galaxy is moving away from us, and at a speed proportional to its distance from us. It is hard to explain without assuming that the Earth is located at the centre of the Universe. Astrophysicists don’t like to do that, because it violates an assumption we make that the Earth is not located anywhere particularly special (the Copernican principle). The solution to our predicament is that the entire Universe is expanding; that is, every point in space is moving away from every other point!
As bizarre as it sounds, this behaviour had already been predicted, using Einstein’s General theory of Relativity, when Hubble published his results. Hubble’s work provided convincing proof that we live in an expanding Universe.
Hubble’s work also shows us that equation (9) is wrong! Or at least, needs some correction. That’s because the redshifts he measured were very large. For example, the most distant galaxy in Hubble’s sample had a redshift of nearly 4. Since \(z = \frac{\Delta \lambda}{\lambda_0} = \frac{v_r}{c}\), according to equation (9), that would suggest the galaxy was moving away from us at nearly 4 times the speed of light! Since nothing can go faster than light, clearly something is wrong with our formula for Doppler shift. In fact, the problem is that we need to make corrections to take account of special relativity. Since that is beyond the level of this course, I will just give the answer here, in the relativistic Doppler equation
This equation should be used in place of equation (9) whenever the radial velocity is a significant fraction of the speed of light (or \(z \geq 0.1\)). Of course, one consequence of an expanding Universe is that it has a finite age. The inverse of the present value of the Hubble constant, \(H_0 \sim 70\) km/s/Mpc, is known as the Hubble time, \(t_{\rm H} \sim 1.4 \times 10^{10}\) yr, which is closely related to the age of the Universe (this requires cosmological parameters that you will come across in third year).
Figure 16 seeks to place this ridiculously large number into context.
One of the primary objectives of the NASA/ESA/CSA James Webb Space Telescope has been to detect and analyse the first galaxies in the Universe, whose rest frame UV and optical light have been redshifted into the infrared. As of December 2022, imaging (using NIRCam) and spectroscopy (using NIRSpec) from the JADES survey has revealed galaxies at redshifts \(z = 10-13\), dating back to a few hundred million years after the Big Bang (Figure 17)
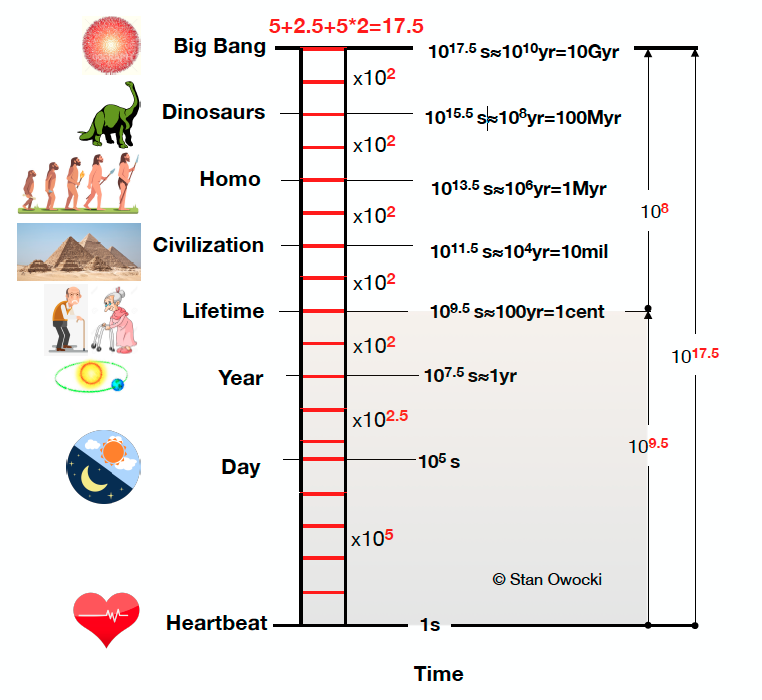
Fig. 16 The age of the Universe compared with more familiar units of time. Courtesy Stan Owocki (Bartol).#
The age of the Universe compared with more familiar units of time
Note that I’ve been spelling Doppler shift with a capital D. That’s because it is named after it’s discoverer, Christian Doppler. Doppler originally proposed it (in 1842) as an explanation of why different stars had different colours. With our modern understanding of Doppler shift, we know that the colour of stars is not caused by Doppler shift. Some of the fastest moving stars in the Galaxy have velocities of 300 km s-1. At the centre of the optical waveband (500 nm) this velocity would cause a Doppler shift of only 0.5 nm; nowhere near enough to significantly change the colour of a star. We need to find a different explanation for the colours of stars.
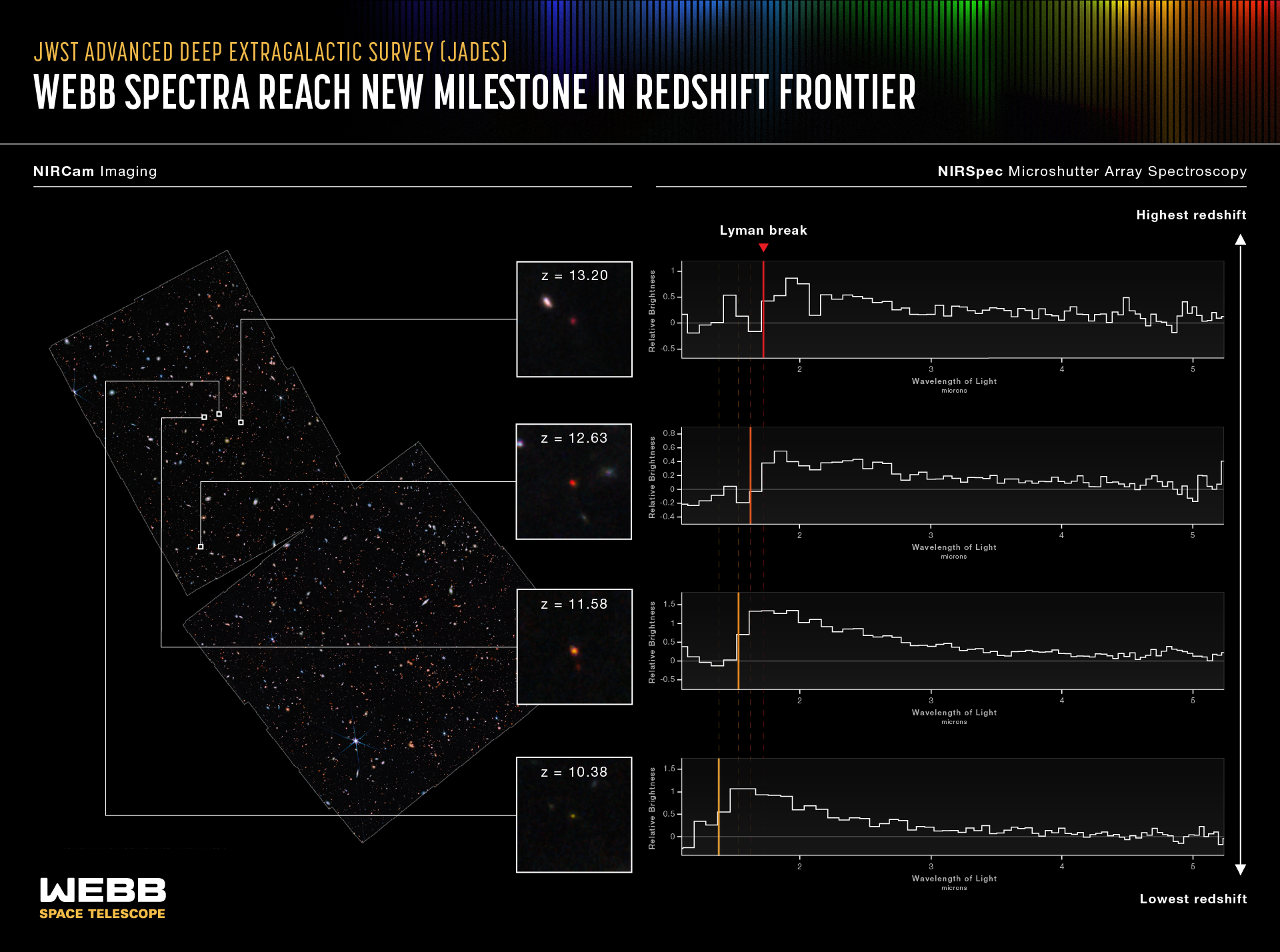
Fig. 17 JWST NIRCam (imaging) and NIRSpec (spectroscopy) of galaxies at redshifts of \(z= 10-13\), dating back to a few hundred Myr after the Big Bang. Image credit: NASA/ESA/CSA, M. Zamani (ESA/Webb), L Hustak (STScI).#
High redshift galaxies discovered by JWST’s JADES survey
